Problems tagged with "gradient descent"
Problem #009
Tags: gradient descent, perceptrons, gradients
Suppose gradient descent is to be used to train a perceptron classifier \(H(\vec x; \vec w)\) on a data set of \(n\) points, \(\{\nvec{x}{i}, y_i \}\). Recall that each iteration of gradient descent takes a step in the opposite direction of the ``gradient''.
Which gradient is being referred to here?
Solution
The gradient of the empirical risk with respect to \(\vec w\)
Problem #028
Tags: gradient descent
Consider the function \(f(x, y) = x^2 + xy + y^2\). Suppose that a single iteration of gradient descent is run on this function with a starting location of \((1, 2)^T\) and a learning rate of \(\eta = 1/10\). What will be the \(x\) and \(y\) coordinates after this iteration?
Solution
\(x = 0.6\), \(y = 1.5\)
Problem #068
Tags: gradient descent
Recall that a subgradient of the absolute loss is:
Suppose you are running subgradient descent to minimize the risk with respect to the absolute loss in order to train a function \(H(x) = w_0 + w_1 x\) on the following data set:

Suppose that the initial weight vector is \(\vec w = (0, 0)^T\) and that the learning rate \(\eta = 1\). What will be the weight vector after one iteration of subgradient descent?
Solution
To perform subgradient descent, we need to compute the subgradient of the risk. The main thing to remember is that the subgradient of the risk is the average of the subgradient of the loss on each data point.
So to start this problem, calculuate the subgradient of the loss for each of the three points. Our formula for the subgradient of the absolute loss tells us to compute \(\Aug(\vec x) \cdot w - y\) for each point and see if this is positive or negative. If it is positive, the subgradient is \(\Aug(\vec x)\); if it is negative, the subgradient is \(-\Aug(\vec x)\).
Now, the initial weight vector \(\vec w\) was conveniently chosen to be \(\vec 0\), meaning that \(\operatorname{Aug}(\vec x) \cdot\vec w = 0\) for all of our data points. Therefore, when we compute \(\operatorname{Aug}(\vec x) \cdot\vec w - y\), we get \(-y\) for every data point, and so we fall into the second case of the subgradient formula for every data point. This means that the subgradient of the loss at each data point is \(-\operatorname{Aug}(\vec x)\). Or, more concretely, the subgradient of the loss at each of the three data points is:
\((-1, -1)^T\)\((-1, -2)^T\)\((-1, -3)^T\) This means that the subgradient of the risk is the average of these three:
The subgradient descent update rule says that \(\vec w^{(1)} = \vec w^{(0)} - \eta\vec g\), where \(\vec g\) is the subgradient of the risk. The learning rate \(\eta\) was given as 1, so we have \(\vec w^{(1)} = \vec w^{(0)} - \vec g = \vec 0 - \begin{bmatrix}-1\\ -2 \end{bmatrix} = \begin{bmatrix}1\\ 2 \end{bmatrix}\).
Problem #085
Tags: gradient descent, subgradients
Recall that a subgradient of the absolute loss is:
Suppose you are running subgradient descent to minimize the risk with respect to the absolute loss in order to train a function \(H(x) = w_0 + w_1 x\) on the following data set:
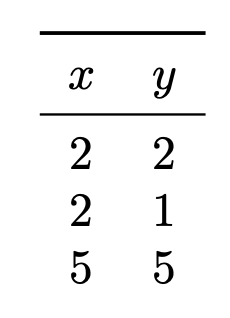
Suppose that the initial weight vector is \(\vec w = (0, 0)^T\) and that the learning rate is \(\eta = 1\). What will be the weight vector after one iteration of subgradient descent?